An Introduction to Six Sigma Management
Add bookmark
Non-Technical Definitions of Six Sigma Management
Editor's note: if you're new to the field of Six Sigma, you might want to consider joining PEX Masters 2012 - an online presentation series that brings you indepth case studies and key skills to help you better manage Six Sigma and process excellence programs/projects. The online event takes place 5-15 November 2012.
Six Sigma management uses statistical process control to relentlessly and rigorously pursue the reduction of variance and standard deviation in all critical processes to achieve continuous and breakthrough improvements that impact the bottom-line and/or top-line of the organization and increase customer satisfaction.
Another common definition of Six Sigma management is that it is an organizational initiative designed to create manufacturing, service and administrative processes that produce a high rate of sustained improvement in both defect reduction and cycle time (e.g., when Motorola began their effort the rate they chose was a 10-fold reduction in defects in two years, along with a 50 percent reduction in cycle).
For example, a bank takes 60 days on average to process a loan with a 10 percent rework rate in 2000. In a "Six Sigma" organization, the bank should take no longer than 30 days, on average, to process a loan with a 1 percent error rate in 2002, and no more than 15 days, on average, to process a loan with a 0.10 percent error rate by 2004. Clearly, this requires a dramatically improved/innovated loan process.
Technical Definition of "Six Sigma" Management
The Normal Distribution
—The term "Six Sigma" is derived from the normal distribution used in statistics. Many observable phenomena can be graphically represented as a bell-shaped curve or a normal distribution as illustrated in Figure 1:
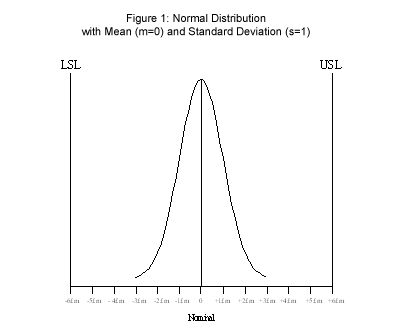
Figure 1: Normal Distribution with Mean (m=0) and Standard Deviation (s=1)
When measuring any process, it can be shown that its outputs (services or products) vary in size, shape, look, feel or any other measurable characteristic. The typical value of the output of a process is measured by a statistic called the mean or average.
The variability of the output of a process is measured by a statistic called the standard deviation. In a normal distribution, the interval created by the mean plus or minus two standard deviations contains 95.44 percent of the data points, or 45,600 data points per million (or sometime called defects per million opportunities denoted DPMO) are outside of the area created by the mean plus or minus two standard deviations [(1.00-.9544= .0456)x1,000,000=45,600].
In a normal distribution the interval created by the mean plus or minus three standard deviations contains 99.73 percent of the data, or 2,700 DPMO are outside of the area created by the mean plus or minus three standard deviations [(1.00-.9973=.0027)x1,000,000 = 2,700]. In a normal distribution the interval created by the mean plus or minus six standard deviations contains 99.9999998 percent of the data, or two data points per billion data points outside of the area created by the mean plus or minus six standard deviations.
[eventPDF]
Six Sigma management promotes the idea that the distribution of output for a stable normally distributed process (Voice of the Process) should be designed to take up no more than half of the tolerance allowed by the specification limits (Voice of the Customer). Although processes may be designed to be at their best, it is assumed that over time the processes may increase in variation. This increase in variation may be due to small variation with process inputs, the way the process is monitored, changing conditions, etc. The increase in process variation is often assumed for the sake of descriptive simplicity to be similar to temporary shifts in the underlying process mean. The increase in process variation has been shown in practice to be equivalent to an average shift of 1.5 standard deviations in the mean of the originally designed and monitored process
If a process is originally designed to be twice as good as a customer demands (i.e., the specifications representing the customer requirements are six standard deviations from the process target), then even with a shift, the customer demands are likely to be met. In fact, even if the process shifted off target by 1.5 standard deviations there are 4.5 standard deviations between the process mean (m + 1.5s) and closest specification (m + 6.0s), which result in at worst 3.4 DPMO at the time the process has shifted or the variation has increased to have similar impact as a 1.5 standard deviation shift.
In the 1980s, Motorola demonstrated that a 1.5 standard deviation shift was in practice was observed as the equivalent increase in process variation for many processes that were benchmarked. Figure 2 shows the "Voice of the Process" for an accounting function with an average of seven days, a standard deviation of one day, and a stable normal distribution. It also shows a nominal value of seven days, a lower specification limit of four days, and an upper specification limit of 10 days. The accounting function is referred to as a three-sigma process because the process mean plus or minus three standard deviations is equal to the specification limits, in other terms, USL= µ+3σ and LSL = µ–3σ. This scenario will yield 2,700 defects per million opportunities or one early or late monthly report in 30.86 years [(1/0.0027)/12].
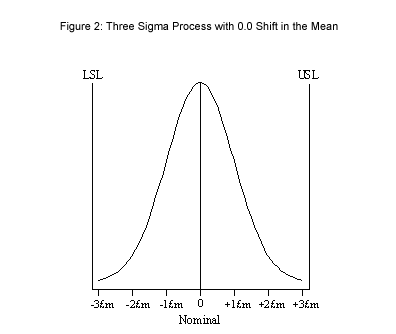
Figure 2: Three Sigma Process with 0.0 Shift in the Mean
Figure 3 shows the same scenario as in Figure 2, but the process mean shifts by 1.5 standard deviations (the process average is shifted down or up by 1.5 standard deviations [or 1.5 days] from 7.0 days to 5.5 days or 8.5 days) over time. This is not an uncommon phenomenon. The 1.5 standard deviation shift in the mean results in 66,807 defects per million opportunities, or one early or late monthly report in 1.25 years [(1/.066807)/12].
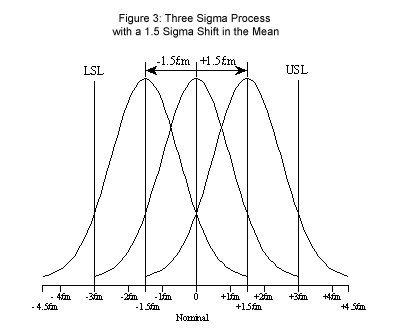
Figure 3: Three Sigma Process with a 1.5 Sigma Shift in the Mean
Figure 4 shows the same scenario as Figure 2 except the Voice of the Process only takes up half the distance between the specification limits. The process mean remains the same as in Figure 2, but the process standard deviation has been reduced to one half-day through application of process improvement. In this case, the resulting output will exhibit 2 defects per billion opportunities, or one early or late monthly report in 41,666,667 years [(1/.000000002)/12].
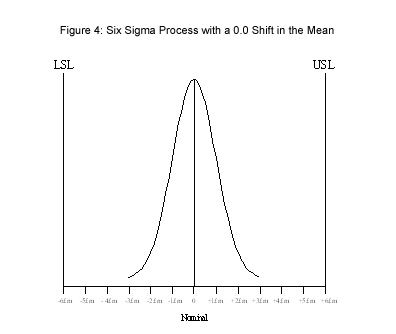
Figure 4: Six Sigma Process with a 0.0 Shift in the Mean
Figure 5 shows the same scenario as Figure 4, but the process average shifts by 1.5 standard deviations (the process average is shifted down or up by 1.5 standard deviations [or 0.75 days = 1.5x0.5 days] from 7.0 days to 6.25 days or 7.75 days) over time. The 1.5 standard deviation shift in the mean results in 3.4 defects per million opportunities, or one early or late monthly report in 24,510 years [(1/.0000034/12]. This is the definition of Six Sigma level of quality.
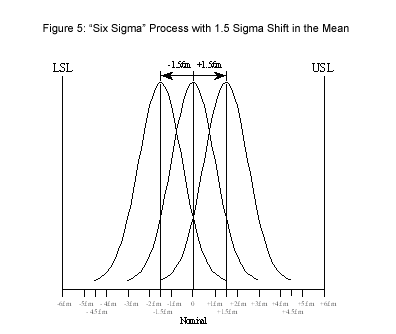
Figure 5: "Six Sigma" Process with 1.5 Sigma Shift in the Mean
Don't forget to register for PEX Masters 2012. The online event takes place 5-15 November 2012.
References:
Gitlow, H., Oppenheim, A., Oppenheim, R. and Levine, D., Quality Management: Tools and Methods for Improvement, 3rd ed. (New York: McGraw-Hill-Irwin, 2004)





















